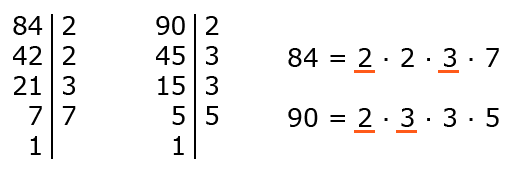НОД это важный математический инструмент
Когда мы решаем задачи, связанные с дробями, делимостью или упрощением выражений, знание НОД (наибольшего общего делителя) становится неотъемлемой частью процесса. Итак, НОД это наибольшее число, на которое оба заданных числа делятся без остатка. Эта концепция, несмотря на свою простоту, играет важнейшую роль как в повседневной жизни, так и в более сложных математических задачах.
Как найти НОД?
Существует несколько методов нахождения НОД, и мы рассмотрим некоторые из них, чтобы вы могли выбрать наиболее подходящий для конкретной задачи.
Метод факторизации
Этот метод заключается в разложении чисел на простые множители и нахождении произведения общих множителей. Рассмотрим это на примере.
- Рассмотрим два числа: 48 и 180.
- Разложим их на простые множители:
- 48 = 24 × 3
- 180 = 22 × 32 × 5
- Общими множителями являются 2 и 3. Выбираем наименьшую степень всех общих множителей: 22 и 31.
- НОД будет 22 × 3 = 4 × 3 = 12.
Алгоритм Евклида
Этот метод считается одним из самых эффективных и простых. Он заключается в последовательном делении большего числа на меньшее и взятии остатка до тех пор, пока остаток не станет равным нулю. Например:
- Возьмем числа 48 и 180.
- Разделим 180 на 48, получим остаток 36.
- Теперь разделим 48 на 36, остаток будет 12.
- Так как 12 без остатка делится на 36, следующий шаг — делим 36 на 12, получаем остаток 0.
- Последний ненулевой остаток, 12, это и есть НОД.
Применение НОД в реальной жизни
НОД это не только теоретическая концепция, но и инструмент, который находит применение в реальных задачах. Вот несколько примеров:
| Сфера применения | Примеры задач |
|---|---|
| Арифметика и дроби | Сокращение дробей при уравнениях или преобразовании числовых выражений. |
| Криптография | НОД используется в алгоритмах шифрования, таких как RSA, для нахождения обратных чисел. |
| Музыка и гармония | При создании музыкальных ритмов для нахождения наибольших общих множителей для правильного построения гармоний. |
Почему важно понимать НОД?
Обучаясь математике, изучение основ, к которым относится и НОД, помогает в дальнейшем более глубоком понимании чисел и операций над ними. Это также учит нас решать задачи, что важнее всего в логике и аналитическом мышлении.
Правильное использование НОД может значительно упростить и ускорить как учебные процессы, так и практические решения в жизни, от финансовых расчетов до технических наук.
Надеемся, что ваше понимание того, что НОД это, стало глубже, и это поможет вам в дальнейших математических путешествиях.