Різниця множин: Основи та Приклади
Одним із фундаментальних понять теорії множин у математиці є різниця множин. Це поняття дозволяє виконувати різноманітні операції над множинами, полегшуючи аналіз і роботу з даними.
Що таке множина?
Перш ніж заглиблюватись у поняття різниці множин, важливо розуміти, що таке множина. У математиці множина визначається як сукупність елементів, які зазвичай мають спільні характеристики. Наприклад, множина {1, 2, 3, 4} складається з чотирьох цілих чисел.
Визначення різниці множин
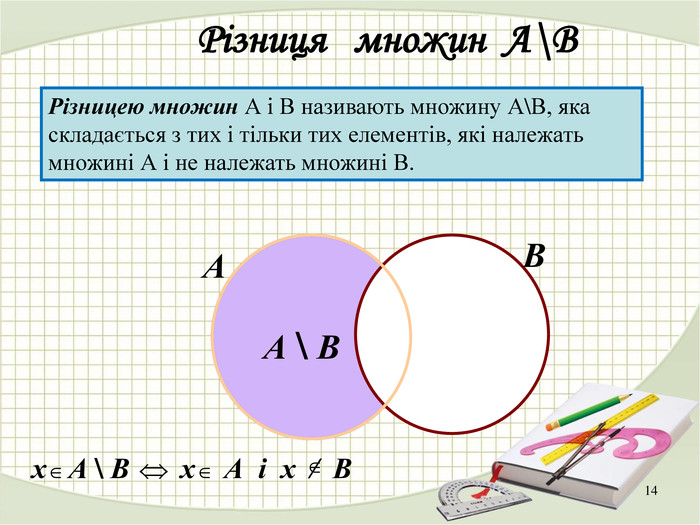
Різниця множин A і B, позначається як A B, – це множина елементів, які належать множині A, але не належать множині B. Ця операція є асиметричною, тобто A B та B A можуть суттєво відрізнятися.
Властивості різниці множин
- Необов’язковість комутативності: A B ≠ B A. Це означає, що змінивши множини місцями, результат також зміниться.
- Необов’язковість асоціативності: (A B) C ≠ A (B C). Це значить, що порядок виконання операцій може впливати на результат.
- Зв’язок з перетином: A B = A (A ∩ B). Це вказує на те, що різниця множин може бути виявлена шляхом виключення перетину множин із першої множини.
Приклади для кращого розуміння різниці множин
- Нехай A = {1, 2, 3, 4} і B = {3, 4, 5, 6}. Тоді A B = {1, 2}, бо 1 та 2 є в A, але не в B.
- Для тих же множин B A = {5, 6}, оскільки 5 і 6 є в B, але не в A.
- Якщо A = {a, b, c} та B = {}, тоді A B = {a, b, c}, оскільки в B немає елементів, які слід віднімати.
Різниця множин у комп’ютерних науках
У комп’ютерних науках концепція різниці множин часто використовується у програмах для обробки та аналізу даних. Наприклад, при побудові індексів для швидкого пошуку даних, досить часто виникає потреба у виключенні дублюючих даних із різних джерел. Різниця множин полегшує цю задачу за рахунок видалення небажаних чи повторюваних елементів.
Використання таблиць для наочності
| Множина A | Множина B | Різниця AB | Різниця BA |
|---|---|---|---|
| {1, 2, 3, 4} | {3, 4, 5, 6} | {1, 2} | {5, 6} |
| {a, b, c} | {b, c, d} | {a} | {d} |
Практичне застосування різниці множин
Різниця множин знайшла широке застосування у різних галузях науки та техніки. В області баз даних, вона використовується для виконання операцій над наборами записів, особливо коли йдеться про виділення унікальних наборів даних.
Завдяки зрозумілому визначенню та широким можливостям застосування, різниця множин залишається важливою частиною аналітичного інструментарію в багатьох наукових і практичних сферах.